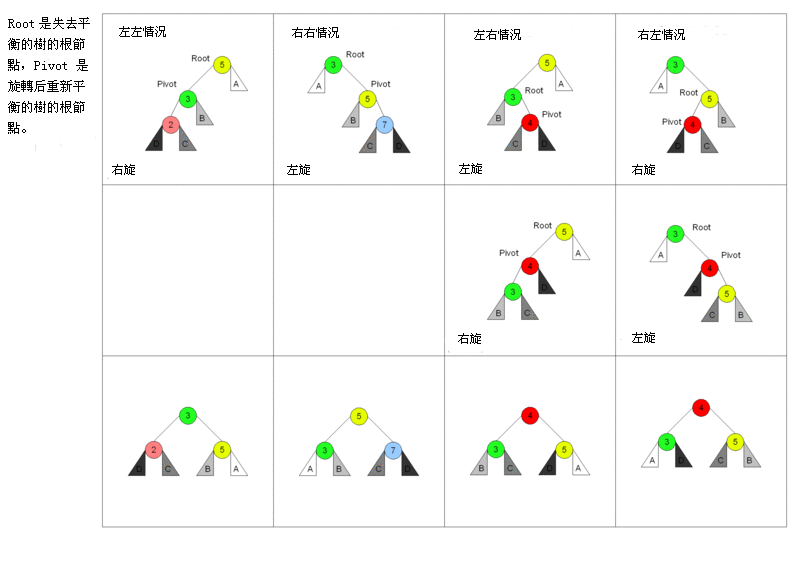
什么是AVL树
介绍AVL树之前先简单了解平衡二叉搜索树。平衡二叉搜索树具有以下性质:它是一颗空树或者它的左右两个子树的高度的绝对值不超过1,并且左右两个子树都是一个平衡二叉树。AVL是最先发明的自平衡二叉树算法。在AVL中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。查找,插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或者多次旋转来重新平衡这个树。
代码实现
package test.algorithm.FastSlowPointer;import test.algorithm.FastSlowPointer.BinarySortTree.BiTNode;public class AVLTree { class BiTNode{ static final int LH = 1; static final int EH = 0; static final int RH = -1; private int data; private BiTNode parent; private BiTNode lChild; private BiTNode rChild; //平衡因子(值为-1、0、1,非这三个值必须要旋转,计算公式为左子树层次数减去右子树层次数) private int bf; public BiTNode(int data,int bf,BiTNode parent){ this.data = data; this.bf = bf; this.parent = parent; } } //树的根节点 private BiTNode root; /** * 平衡而二叉树的插入操作 * 基本原理为: * 1.首先如同二叉排序树一般,找到其要插入的节点的位置,并把元素插入其中; * 2.自下向上进行回溯,回溯做两个事情: * (1)其一是修改祖先节点的平衡因子,当插入 一个节点时只有根节点到插入节点 * 的路径中的节点的平衡因子会被改变,而且改变的原则是当插入节点在某节点(称为A) * 的左子树 中时,A的平衡因子(称为BF)为BF+1,当插入节点在A的右子树中时A的BF-1, * 而判断插入节点在左子树中还是右子树中只要简单的比较它与A的大小 * (2)在改变祖先节点的平衡因子的同时,找到最近一个平衡因子大于2或小于-2的节点, * 从这个节点开始调整最小不平衡树进行旋转调整,关于如何调整见下文。 * 由于调整后,最小不平衡子树的高度与插入节点前的高度相同,故不需继续要调整祖先节点。 * 这里还有一个特殊情况,如果调整BF时,发现某个节点的BF变为0了,则停止向上继续调整, * 因为这表明此节点中高度小的子树增加了新节点,高度不变,那么祖先节点的BF自然不变。 * */ public boolean insert(int key){ if(root==null){ //树为空的时候,添加到根节点 root = new BiTNode(key,0,null); return true; } //当前遍历的节点 BiTNode curr = root; //要插入节点的父节点 BiTNode parent = null; do{ parent = curr; if(key curr.data){ // 往右子树找 curr = curr.rChild; }else{ // 找到,插入失败 return false; } }while(curr!=null); //插入节点 if(key / \ \ * ll rd ll rdl tr * / * rdl * * * 情况2(rd的BF为0) * t rd * / \ / \ * l tr 左旋后右旋 l t * / \ -------> / \ / \ * ll rd ll rdl rdr tr * / \ * rdl rdr * * * 情况3(rd的BF为-1) * t rd * / \ / \ * l tr 左旋后右旋 l t * / \ -------> / / \ * ll rd ll rdr tr * \ * rdr * * * 情况4(L等高) * t l * / 右旋处理 / \ * l ------> ll t * / \ / * ll rd rd * */ private boolean leftBalance(BiTNode t){ // 标记树的高度是否改变 boolean taller = true; BiTNode l = t.lChild; switch (l.bf) { //左高,右旋调整,旋转后树的高度减小(左左情况,见图) case BiTNode.LH : t.bf = BiTNode.EH; l.bf = BiTNode.EH; rotateRight(t); break; //右高,分情况调整 (左右情况,见图) case BiTNode.RH : BiTNode rd = l.rChild; //调整各个节点的BF switch(rd.bf){ //参见方法注释情况1 case BiTNode.LH : t.bf = BiTNode.RH; l.bf = BiTNode.EH; break; //参见方法注释情况2 case BiTNode.EH : t.bf = BiTNode.EH; l.bf = BiTNode.EH; break; //参见方法注释情况3 case BiTNode.RH : t.bf = BiTNode.EH; l.bf = BiTNode.LH; break; } //先左旋再右旋 rd.bf = BiTNode.EH; rotateLeft(t.lChild); rotateRight(t); break; //特殊情况4,这种情况在添加时不可能出现, //只在移除时可能出现,旋转之后整体树高不变 //删除root的右孩子 case BiTNode.EH : t.bf = BiTNode.LH; l.bf = BiTNode.RH; rotateRight(t); taller = false; break; } return taller; } /** * 最小旋转子树的根节点 * 向右旋转之后,p移到p的右子节点处,p的左子树l变为最小旋转子树的根节点 * l的右子节点变为p的左节点、 * 例如: p(2) l(-1) * / 右旋转 / \ * l(0) ------> / p(0) * / \ / / * lL(0) lR(0) lL(0) lR(0) */ private void rotateRight(BiTNode p){ System.out.println("绕"+p.data+"右旋"); if(p!=null){ BiTNode l = p.lChild; //p的父节点赋给l的父节点 l.parent = p.parent; //把l的右节点lR作为p的左节点 p.lChild = l.rChild; if(l.rChild!=null){ l.rChild.parent = p; } if(p.parent==null){ //p是根节点,重新设置根节点 root = l; }else if(p.parent.rChild==p){ //p是父节点右子树的根节点,重新设置左子树的根节点 p.parent.rChild = l; }else{ //p是父节点左子树的根节点,重新设置左子树的根节点 p.parent.rChild = l; } //p为l的右子树 l.rChild = p; //设置p的父节点为l p.parent = l; } } /** * 最小旋转子树的根节点 * 向左旋转之后p移到p的左子树处,p的右子树B变为此最小子树根节点, * B的左子树变为p的右子树 * 比如: p(-2) r(1) * \ 左旋转 / \ * r(0) ----> p(0) \ * / \ \ \ * rL(0) rR(0) rL(0) rR(0) * 旋转之后树的深度之差不超过1 */ private void rotateLeft(BiTNode p){ System.out.println("绕"+p.data+"左旋"); if(p!=null){ BiTNode r = p.rChild; //p的父节点赋给r的父节点 r.parent = p.parent; //把r的左节点rR作为p的右节点 p.rChild = r.lChild; if(r.lChild!=null){ r.lChild.parent = p; } if (p.parent == null) //p是根节点 ,r变为父节点,即B为父节点 root = r; else if (p.parent.lChild == p) //p是左子节点 ,p的父节点的左子树为r p.parent.lChild = r; else //如果p是右子节点 p.parent.rChild = r; //p为r的左子树 r.lChild = p; //设置p的父节点为r p.parent = r; } } /** * 做右平衡处理 * 平衡因子的调整如图: * 情况1(ld的BF为1) * t ld * / \ / \ * tl r 先右旋再左旋 t r * / \ --------> / \ \ * ld rr tl ldl rr * / * ldl * * 情况2(ld的BF为0) * t ld * / \ / \ * tl r 先右旋再左旋 t r * / \ --------> / \ / \ * ld rr tl ldl ldr rr * / \ * ldl ldr * * 情况3(ld的BF为-1) * t ld * / \ / \ * tl r 先右旋再左旋 t r * / \ --------> / / \ * ld rr tl ldr rr * \ * ldr * * 情况4(r的BF为0) * t r * \ 左旋 / \ * r -------> t rr * / \ \ * ld rr ld * */ private boolean rightBalance(BiTNode t){ //记录树的层次变化 boolean heightLower = true; BiTNode r = t.rChild; switch(r.bf){ //左高,分情况调整(右左情况) case BiTNode.LH: BiTNode ld = r.lChild; //调整各个节点的BF switch(ld.bf){ //参见方法注释情况1 case BiTNode.LH : t.bf = BiTNode.EH; r.bf = BiTNode.RH; break; //参见方法注释情况2 case BiTNode.EH : t.bf = BiTNode.EH; r.bf = BiTNode.EH; break; //参见方法注释情况3 case BiTNode.RH : t.bf = BiTNode.LH; r.bf = BiTNode.EH; break; } ld.bf = BiTNode.EH; rotateRight(t.rChild); rotateLeft(t); break; //右高,左旋调整(右右情况) case BiTNode.RH: t.bf = BiTNode.EH; r.bf = BiTNode.EH; rotateLeft(t); break; //特殊情况4 case BiTNode.EH: r.bf = BiTNode.LH; t.bf = BiTNode.RH; rotateLeft(t); heightLower = false; break; } return heightLower; } /** * 查找指定元素,如果找到返回其BiTNode对象,否则返回null */ public BiTNode search(int key){ BiTNode node = root; while(node!=null){ if(key==node.data){ return node; }else if(key PS:下图表以四列表示四种操作,每行表示在该种情况下要进行的操作。在左左和右右的情况下,只需进行一次旋转操作;在左右和右左的情况下,需要进行两次操作。